Why Care Block?
I applaud all of you who have made it this far, but unfortunately things are going to get super boring! Well, besides applause I’d also like to take a sentence to thank you for reading this content: whether you’re reading this out of boredom, coercion, to make fun of it, or you just have a general interest, I’d like to extend my gratitude.
Switching back to the good stuff, today we’re talking about hash functions. Think hash browns *delicious* - they’re sliced, diced, and fried to a golden brown; drenched or drizzled with hot sauce or ketchup (I prefer Cholula and Tabasco) and resembles nothing like the raw potato it once was. Now, take your hash browns and try to reconstruct the original potato. “No!” you’d say, “That’s really hard.” Keep in mind this post is about security, from a non-cryptographic scientist or security expert, so anticipate a lot more potato metaphors because that’s about all I know about security. This post is really about making the Twitter API work within Stata without any outside plugins or packages. To do so, we must find a way to recreate the HMAC-SHA1 algorithm which is quite difficult without our previous toolset we designed, so make sure you’ve gone over the bitwise operators. Once we’re on the same page, we can start getting into this hash function in order to send requests using Twitter’s API so that you can retrieve you beautiful, crispy hash brown data in return. The Fuss
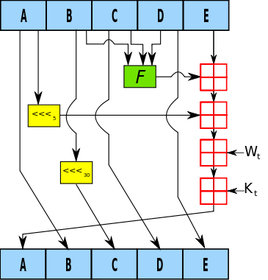
HMAC-SHA1 is the type of procedure we’re trying to reproduce from the Wikipedia article available here. I didn’t care much for it. It didn’t explain what it is, what it was really doing, or why we should care at a simple level so that someone less savvy (like me) could understand just what the fuss is all about. Both HMAC and SHA1 are procedures. HMAC stands for Hash Message Authentication Code and is the procedure we use to combine a message with a secret key whereas SHA-1 stands for Security Hash Algorithm 1, which was made by the NSA and is used to break a message into a corresponding hash string with a fixed block size. Together, they make sure that the integrity of the data hasn’t been compromised and that you’re not sending your raw secret message over the internet…series of tubes. The nice thing about the SHA-1 algorithm is that very slight changes, say replacing a single character in the message, dramatically changes the resulting hash so that it’s difficult to crack (though apparently not secure enough for today’s standards). Remember, HMAC is the main procedure to combine a secret key with the message and SHA-1 is just the type of hash function implemented; but you probably don’t care that much and just want to see the code. So let’s get started!
The SHA-1
SHA-1 has a lot of destructive procedures, a lot of breaking bits into smaller bits, and a lot of the previously developed bitwise functions. Let’s see a quick example of this in action.
Say I have the string phrase "The Ore-Ida brand is a syllabic abbreviation of Oregon and Idaho" and I want to run the SHA-1 Function on it.
mata: sha1("The Ore-Ida brand is a syllabic abbreviation of Oregon and Idaho")
The results is (hex): 156a5e19b6301e43794afc5e5aff0584e25bfbe7
In Base64: FWpeGbYwHkN5SvxeWv8FhOJb++c=
Good luck figuring out the original string from the Base64 encoding. Now remember, this is not a post about theory or reasoning behind the SHA-1 procedure; this post is about making it work. Therefore, the advanced Stata user who wishes to replicate/improve this code might find this next section interesting. Here are some of my observations regarding repackaging the SHA-1 function.
The HMAC
Compared to SHA-1, the HMAC procedure is a walk in the potato fields… it’s easy as potatoes… I’m running out of references here. Did you know that the potato was the first vegetable to be grown in space? If astronauts could do that with potatoes, we can certainly make HMAC-SHA1 work with Stata. There’s really just a three step process at play. The HMAC procedure takes two inputs: a key and a message.
The Conclusion
Well, this post (and the previous one) has been filled with a little more technical jargon than I planned. I like to keep these posts fun and poignant, but this material is for the dedicated and serves as a reference for those who want to expand Stata’s capabilities (even if it takes a little longer than expected). This new Mata function allows Stata to perform the HMAC-SHA1 procedure which is vital for enabling Twitter requests through Stata so that the entire process can be contained within one do-file. Here’s an example of the function in action:
. mata: hmac_sha1("Secret Key", "Message to be sent")
d5052c13e868ea7c932be9279752e9e67c8195bd
. mata: hmac_sha1("Secret Key", "Message to be Sent")
f67f5f90132583de85abf0d61fed2a2144be1f04
You can see how the examples show that slight changes in the message dramatically change the output. Feel free to download the process below. All subroutines are included for your convenience. Good luck!
5 Comments
Bitwise Operators (aka Bits, Bits, Bits Part II)
Did you know that Mata supports bitwise operators? Well, it actually doesn't – in the typical sense. But that won't stop us from making it work. You see, Mata can handle data extremely well, and with a little finesse, can be forced to do things it wasn't really made to do. Yes it's going to be slow, and yes it's probably not very useful to the average user, but let me try to convince you how great using Mata really is!
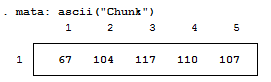
For those who don't know, Mata is a lower level language than Stata – many of Stata's complex functions are actually written in Mata because it's really quite fast. Mata mimics a lot of C's syntax, but also simplifies things so you don't feel like you have to explicitly declare everything. In previous posts we've exploited the power of the - inbase() - function and we will make ample use of that today. Say we have a text file containing the word "Chunk". While we see a word, the computer sees numbers which correspond to each letter – otherwise known as ASCII. Mata's - ascii() - function can help us find this representation:
This is a simple way of converting our text into numbers, but how about into bytes? Typically, bytes are displayed in base 16:
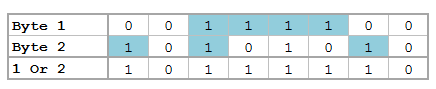
But now we want to see each bit. Remember, I'm not a computer scientist, so you can trust me when I say this really isn't all that bad for those of you who haven't been exposed to this stuff. Just know that each of these bytes contains 8 bits. Each bit can either be on or off (1 or 0) which means that there’s a total possible bit combination of 2^8 = 256 per byte. Let's look at what Stata shows us when we look at everything in base 2:
Notice, I added a zero and a one at the end of the text string "chunk" for illustrative purposes. Why are these values not 0 and 1 respectively? That’s because the digits are also ASCII characters (digits 48 and 49). We can get the values of zero and one by using the - char() - function. For fun, we'll also look at values two and three as well.
Well, because there are technically 8 bits per byte, we need to pad each output with zeros so that the total length is 8 bits. For example: the value "3" can be written as "11" in base 2, but is the same "00000011" so that we can imagine all 8 bits. We can easily accomplish this in matrix form.
Notice the use of the colon operator? It's by far one of my favorite operands (not that I have that many) because it does the same operation on each element of the matrix, which makes the overall statement extremely succinct! The statement above just says: "Give me some zeros, exactly 8 minus how every many numbers we had, and append the original statement to the end to make sure every element has exactly 8 digits."
We should probably make this into a function, since we’ll use it a lot. So let's make the size of the padding an input as well.
mata:
string matrix padbit(string matrix x, real scalar padnum)
{
string matrix y
y = "0" :* (padnum :- strlen(x)) :+ x
return (y)
}
end
mata: padbit(chunk, 8)
|
|||||||||||||
| bitwise-mata-functions.do | |
| File Size: | 2 kb |
| File Type: | do |
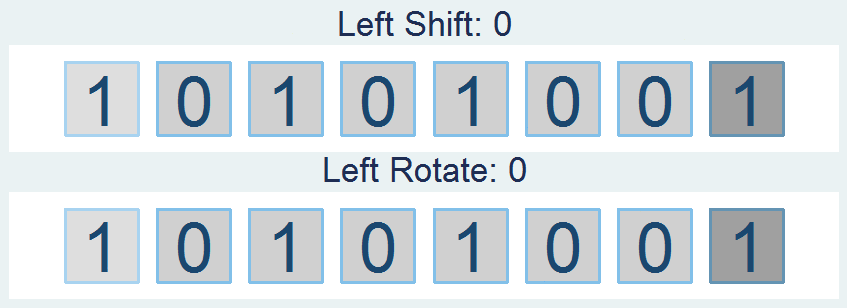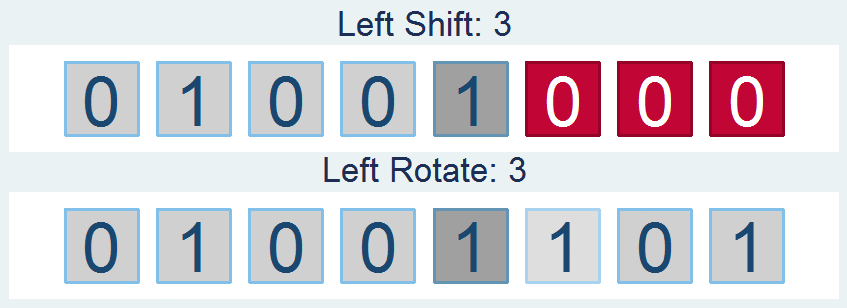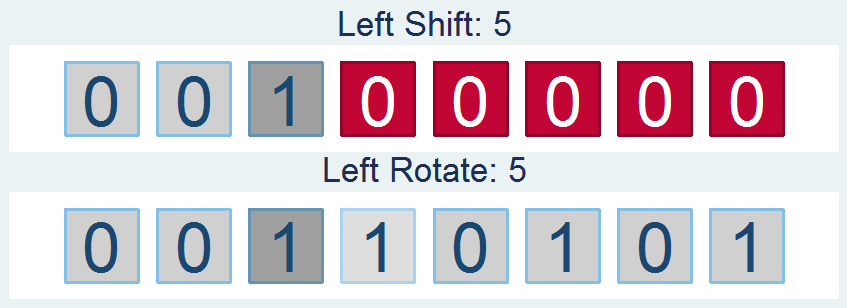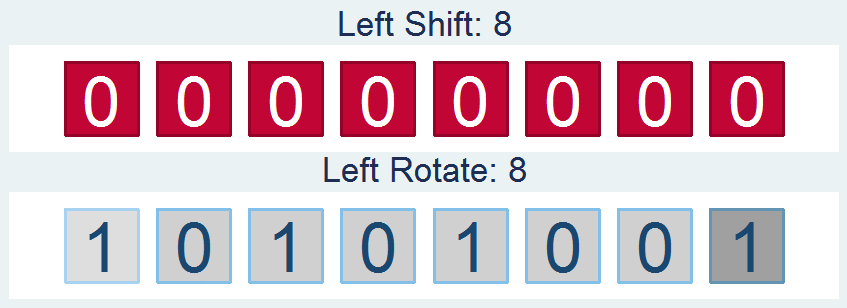
Shifts and Rotations
It's interesting to follow, though not all that interesting if it doesn't have a practical application. If you're like "honestly, I don’t know nothing about bit functions", I'll say - well I've got the one you. How about a way to easily encrypt your files so that you can hide your sensitive stuff in plain sight? First find a file and read it in:
// Read in File to Copy
fh = fopen("Building an API Library.docx", "r")
eof = _fseek(fh, 0, 1)
fseek(fh, 0, -1)
x = fread(fh, eof)
fclose(fh)
Convert the file characters to the ASCII decimal value then convert this number into the base 2 representation (don't forget to pad the bits). From here, we can use our bitwise operations before converting this number back to base 10 and finally back to characters:
// Run Bitwise Not
y = padbit(inbase(2, ascii(x)), 8)
for (i=1; i<=cols(y); i++) {
y[i] = bitnot(y[i])
}
y = char(frombase(2, y))
Lastly, write your newly altered file using Mata. This is obviously very basic, but a great way to hamper nosy coworkers.
// Write the Results to File
fh = fopen("Copy.docx", "w")
fwrite(fh, y)
fclose(fh)
But really, we're doing this with the ultimate goal of gaining access to Twitter data using Twitter's API. This is just step one of a three part series and if you're lost so far. there's plenty of time to see the motivation for this post in the next step. I promise it gets more interesting, yet I hope I've shown some of Mata's potential and how you can easily bring in the concepts to your own do-files.
Author
Will Matsuoka is the creator of W=M/Stata - he likes creativity and simplicity, taking pictures of food, competition, and anything that can be analyzed.
For more information about this site, check out the teaser above!
Archives
July 2016
June 2016
March 2016
February 2016
January 2016
December 2015
November 2015
October 2015
September 2015
Categories
All
3ds Max
Adobe
API
Base16
Base2
Base64
Binary
Bitmap
Color
Crawldir
Email
Encryption
Excel
Exif
File
Fileread
Filewrite
Fitbit
Formulas
Gcmap
GIMP
GIS
Google
History
JavaScript
Location
Maps
Mata
Music
NFL
Numtobase26
Parsing
Pictures
Plugins
Privacy
Putexcel
Summary
Taylor Swift
Twitter
Vbscript
Work
Xlsx
XML


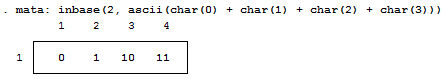




 RSS Feed
RSS Feed